scNET: learning context-specific gene and cell embeddings by integrating single-cell gene expression data with protein–protein interactions

Abstract

Recent advances in single-cell RNA sequencing (scRNA-seq) techniques have provided unprecedented insights into the heterogeneity of various tissues. However, gene expression data alone often fails to capture and identify changes in cellular pathways and complexes, as they are more discernible at the protein level. Moreover, analyzing scRNA-seq data presents further challenges due to inherent characteristics such as high noise levels and zero inflation. In this study, we propose an approach to address these limitations by integrating scRNA-seq datasets with a protein–protein interaction network. Our method utilizes a unique dual-view architecture based on graph neural networks, enabling joint representation of gene expression and protein–protein interaction network data. This approach models gene-to-gene relationships under specific biological contexts and refines cell–cell relations using an attention mechanism. Next, through comprehensive evaluations, we demonstrate that scNET better captures gene annotation, pathway characterization and gene–gene relationship identification, while improving cell clustering and pathway analysis across diverse cell types and biological conditions.

Main

Single-cell RNA sequencing (scRNA-seq) data have revolutionized our understanding of complex biological systems by revealing inherent cellular heterogeneity. Typically, scRNA-seq analysis involves graph-based clustering to identify distinct cell populations, followed by differential gene expression analysis. This approach highlights key genes associated with specific cell states and functions.

One key limitation of scRNA-seq data is its zero-inflated nature¹. These zero counts represent a mix of biological signals and technical limitations, resulting in a notably higher dropout rate compared with bulk RNA sequencing (RNA-seq). This leads to a substantial proportion of false zero values, masking true signals and resulting in a loss of correlation in gene expression², and thus struggles to delineate complexes and pathways activation. Addressing this issue various methods have been developed for scRNA-seq data imputation³. These at large include zero-inflated probabilistic models, nearest-neighbor-based smoothing of expression profiles, and techniques to discover dense latent representations. Although these methods are theoretically capable of revealing gene–gene interactions, most methods focus on numerical recovery of dropout events and cell clustering⁴.

Several other approaches were suggested for tackling specifically the loss of correlation in scRNA-seq data. A model proposed by Aleksander et al.⁵ introduces a cell-specific correlation model that considers sequencing depth and read errors to infer cell-type-specific coexpression. However, these and the above-mentioned approaches aim to separate the true biological signal from noise, without the use of previous and complementary knowledge.

Protein–protein interaction (PPI) networks effectively capture the functional context of genes, including pathway and complex activation as well as signal transduction. A key limitation of these networks is that they are typically constructed on a global scale, capturing interactions at the organism level without reflecting the dynamic changes that occur across different cell types and biological conditions. Therefore, integrating PPIs with scRNA-seq holds great potential, as it combines the dynamic nature of scRNA-seq with the strong functional annotation and contextual information provided by PPI networks, which could enhance downstream scRNA-seq analyses.

In earlier work⁶, we demonstrated the potential of dataset-specific weighted PPIs to identify downstream signaling events following cell–cell interactions. On a broader scope, integrating the connections represented by PPIs into specific datasets may help identify condition-specific gene–gene relationships. This concept has been explored in studies such as that of Zand and Ruan⁷, who proposed the idea of propagating gene expression across PPI edges. Another study⁸ demonstrated how PPI networks can be used with a set of differentially expressed genes to find a subset of key genes that can explain patient’s survival rates in non-small-cell lung cancer. Further research^9,10 has shown that this integration can enhance fundamental scRNA-seq tasks, such as dimensionality reduction, dropout imputation and cell–cell similarity analysis.¹¹ Introduced a non-negative matrix factorization-based framework for incorporating PPIs in the imputation of scRNA data. More recently, Li et al.¹² introduced a graph embedding method called scLINE, which integrates scRNA data with various biological networks to capture gene-to-gene and gene–cell relationships within a dense latent space representation. Still, further methods that can simultaneously learn and refine both gene–gene and cell–cell relationships while embedding network information may be of advantage.

Recent advances in the field of natural language processing and large language models have also been introduced into the domain of scRNA-seq. Whereas works such as that of Yang et al.¹³ focused on specific tasks such as supervised cell annotation, more recent efforts^14,15,16 have focused on developing foundational models trained on extremely large scRNA-seq atlases, comprising tens of millions of cells. Although these models demonstrate strong performance in capturing atlas-scale dynamics, they often require fine-tuning with supervised loss (commonly using cell labels) when applied to specific datasets, which may not be available in most newly sequenced datasets. Thus, an unsupervised framework that can be applied to unlabeled small-to-medium scRNA-seq datasets is called for.

Recently, Li et al.¹⁷ introduced a graph neural network (GNN)-based method (PINNACLE) for learning gene representations by integrating scRNA-seq atlases and PPI networks. Their work demonstrates the advantages of combining scRNA-seq data with PPI information using a deep learning framework at the atlas level. In our presented framework, we aim to showcase the benefits of deep learning-based PPI integration at the dataset level, while also leveraging cell similarity to enhance the learned embeddings effectively.

Here we introduce scNET—a method that combines both gene–gene and cell–cell relations to learn simultaneously gene and cell embeddings. scNET learns GNNs based on protein–protein interactions on the one hand and cell–cell expression similarities on the other hand. Propagating gene expression information on both networks alternately, our proposed framework aims to simultaneously smooth noise and learn condition-specific gene and cell embeddings. It also introduces an edge attention-based mechanism to refine the cell–cell relations graph (K-nearest neighbor, KNN), relaxing the common assumption of a fixed number of connections per cell, which may not align with real biological systems. Our gene-based and cell-based dual view of the expression data facilitates the discovery of both types of relations and their usage in downstream tasks.

Our results indicate that scNET surpasses traditional imputation methods and advanced statistical models in elucidating gene–gene relationships. We also demonstrate the potential of scNET’s cell embedding, leading to better cell clustering. Finally, we show that scNET’s reconstructed gene expression presents a clear advantage in identifying differentially enriched pathways in different cell types and biological conditions.

Results

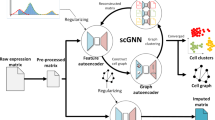
We present scNET—a deep learning framework that employs a dual-view encoder to integrate scRNA-seq data with PPI information (Fig. 1). This approach is designed to elucidate both gene-to-gene and cell-to-cell relationships. Analyses of model loss convergence and running times across different dataset scales are provided in Supplementary Figs. 2–4. We also demonstrate that scNET captures PPI network information contingent upon gene expression data (Supplementary Fig. 5).

Fig. 1: Autoencoder model architecture.

Initially, the PPI network, the KNN graph and gene expression data are input into the dual-view encoder (dashed line). Subsequently, graph attention layers are employed to extract the latent representations of both cells and genes. The inner product decoder is then used to reconstruct the network connections, whereas a fully connected layer is responsible for reconstructing the gene expression. The KNN graph then undergoes pruning using attention coefficients to optimize model performance.

In the following sections, we validate the advantages and accuracy of scNET gene and cell embeddings, pruned KNN graphs and reconstructed gene expression profiles. We show that the learned gene embedding space effectively captures functional groups and coannotations, while the cell embedding captures a refined cell–cell similarity. Moreover, we demonstrate that the reconstructed gene expression profiles offer substantial advantages in standard differential pathway enrichment analyses in scRNA-seq.

scNET gene embedding better captures functional annotation

To evaluate the utility of the acquired embedding space, we first tested whether the correlations in the embedding space accurately reflected known biological annotations and functions. We calculated the Gene Ontology (GO) semantic similarity value^5,18,19 and coembedded coefficient for every gene pair. We then analyzed the distribution of the absolute correlation between these values and compared our results with those from other scRNA-seq data imputation tools, including sct.transform²⁰, SAVER²¹, Magic²², DeepImpute²³, Cell-type-specific correlation tool CSCORE²⁴, the graph embedding tool scLINE¹² and the newly publish fundamental model¹⁴. Our embedding space was characterized by a substantially higher mean correlation, averaging around 0.17, with some genes correlating up to 0.5. This improvement, compared with methods that do not use previous information, is a strong indication of the advantage of deeply integrating biological networks with gene expression data (Fig. 2a).

Fig. 2: Evaluation of gene representation using malaria-associated B cell dataset.

a, Distribution of GO semantic similarity values for different methods, each boxplot presents the 25, 50 and 75 percentiles. b, Percentage of GO enriched clusters as a function of the number of clusters. c–e, UMAP projections of gene representation according to different methods — counts (c), scLINE (d) and scNET (e). Genes are colored by their clusters following a 30-means clustering.

Next, we assessed how well our embedding space captures functional annotations by clustering genes. Using the k-means algorithm with cluster numbers ranging from 20 to 80, we measured the percentage of clusters significantly enriched for one or more GO terms. Enrichment was calculated using the gene set enrichment analysis (GSEA) tool^25,26. A notable improvement was observed across all clustering ranges (Fig. 2b), affirming the enhanced clustering efficacy of scNET gene embedding. A related result appears in Fig. 2c–e, where we present a uniform manifold approximation and projection (UMAP) dimensional reduction of the genes for the counts (Fig. 2c), scLINE (Fig. 2d) and scNET (Fig. 2e) gene embedding spaces. The genes are colored by their k-means clusters (with K = 30). Our scNET embedding captures smaller, more well-defined clusters compared with both the original counts and scLINE. In Supplementary Fig. 6 we present an analysis aiming to show that our gene latent spaces capture different dynamics for different cell types.

Finally, to further demonstrate that scNET gene embeddings better capture functional information, we trained a three-layer multilayer perceptron classifier to predict GO annotations from the embeddings. We focused on GO annotations with at least 50 genes expressed in our dataset to avoid sparsity issues. The classifier was trained using a multilabel cross-entropy loss in a fivefold cross-validation setting. For each fold, we calculated the area under the receiver operating characteristic curve (AUROC) and the area under the precision-recall curve (AUPR). We also benchmarked scNET against three other methods (scGPT, scLINE and DeepImpute). The results demonstrate that scNET embeddings effectively capture functional annotation information in the gene representations (Extended Data Fig. 1).

scNET coembedded network captures biological pathways

Next, we used the learned representation to construct a coembedded network that integrates PPI and coexpression information. We hypothesize that this network could open new avenues for coexpression network analysis in scRNA-seq, as it serves as a strong inference tool in bulk RNA-seq but has not yet been replicated in the domain of single-cell analysis. To this end, we leverage again the malaria-associated B cells dataset, pairwise absolute value correlations were computed in both the original and the embedding space, and thresholds were set at the 50th, 75th, 95th and 99th percentiles. The Leiden²⁷ algorithm was then used to estimate the modularity values of each network (Fig. 3a). Evidently, scNET embedding space-based networks were substantially more modular than their original space counterparts across all resolutions. As the maximum modularity value was attained for both networks when the 99th percentile was employed as the threshold, this specific threshold was applied in the subsequent analyses. A representative sub-network of the resulting coembedded network is shown in Fig. 3b.

Fig. 3: Coembedded network evaluation using malaria-associated B cell dataset.

a, Modularity results for various correlation thresholds. b, Representative sub-network of the co-embedded gene network with annotated lead Leiden clustering. c, AUPR value for KEGG prediction for different methods. d, Distribution of z score results from each of the three tested networks (coembedded, PPI, coexpression) on disease-associated gene lists. Each boxplot presents the 25, 50, 75 percentiles. e, Performance comparison of each network on gene lists associated with blood cancers.

To further evaluate the resulting network, we used a previously described approach²⁸ that attempts to quantify the ability of the network to reconstruct Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways²⁹. We focused on pathways comprising at least 30 genes expressed in the dataset. Each pathway was separated into a training and a test set, where each gene in the training set was assigned a value of 1. These membership values were then propagated (Methods) to score the rest of the genes and evaluate the quality of reconstructing the test set. The results are shown in Fig. 3c, scNET outperforming previous approaches.

Finally, we compared our integrated representation to both the PPI network and the original counts in reconstructing gene lists associated with different diseases³⁰. Unlike KEGG pathways, these lists do not represent clear pathways but rather general associations of genes with conditions, allowing us to validate the performance of our method on less structured lists. To account for the large topological differences between the networks particularly, our coembedded network is much sparser due to the 99% cutoff. We assessed the predictive power of each network against a set of randomized networks (Methods). The coembedded network achieved a mean z score of approximately 7, while the PPI and coexpression networks reached z scores of 3 and 0.5, respectively (Fig. 3d); the full results can be found in Supplementary Fig. 7.

In Fig. 3e, we present the results of each network from different types of leukemias and lymphomas, as those diseases are strongly related to B cells. We observed that, in six out of the nine gene lists tested, our scNET coembedded network performed better than both other networks, while the PPI network achieved the highest score in the remaining three. The count-based coexpression network did not achieve the highest result in any of those lists. These results indicate that our newly integrated embedding performs better than both inputs of our model, demonstrating a synergistic effect in the integration.

In Extended Data Fig. 2, we demonstrate how the coembedded network can be leveraged to identify unique genes that are differentially associated with key molecules under different biological conditions. Specifically, we applied this approach to a mouse glioblastoma multiforme (GBM) dataset³¹, focusing on the CD8⁺ T cell population. As previously described, the P-selectin knockout results in increased infiltration, activation and proliferation of CD8⁺ T cells compared with control CD8⁺ T cells. We sought to determine whether scNET could identify genes differentially associated with the marker of T cell activation and exhaustion PD1 (encoded by Pdcd1), in the control population.

First, we constructed differential coembedded networks using our model to learn distinct coembedded structures for the treatment and control samples. The differential network was then defined by applying the XOR operator to these networks. We focused specifically on the PD1 coinhibitory receptor, hypothesizing that the differential network could reveal genes with altered associations to this receptor. To investigate this, we applied network propagation (Methods) to assign an association (propagation) score to each gene. Our coembedded network effectively captures functional associations and relationships between genes. Thus, this approach would allow us to identify differential functional associations between conditions that may differ from standard DE-based analyses. We observed strong associations with genes involved in cytokine signaling and receptors, such as Il2ra and Ifng, as well as costimulatory genes like Cd28, Tnfrsf9 (also known as 4-1BB) and Tnfsf11. These differential functional associations with costimulatory and T cell activation genes may suggest a more pronounced regulatory role for PD1 in the control condition.

Evaluation of cell clustering

Next, we evaluated the ability of scNET to refine cell–cell similarity by utilizing two datasets from Usoskin et al.³², which include various sensory neurons from the dorsal root ganglia (DRG) and Tian et al.³³, which comprises three different cancer cell lines. These datasets contain ground truth labels (as opposed to postprocessing annotations determined by the analysis pipeline), making them suitable for benchmarking.

For each dataset, we compared the performance of scNET with that of the original counts-based clustering, scLINE¹², the established imputation method MAGIC²² and two state-of-the-art foundational models: scGPT¹⁴ and GeneFormer¹⁵. For the foundational models, we used the pretrained versions without more fine-tuning, as scNET and the other methods operate in an unsupervised manner (which is important since true cell labels are often unavailable for newly generated scRNA-seq datasets). In Fig. 4, we present the UMAP embeddings for each method (scNET, counts, scLINE, MAGIC, scGPT, GeneFormer) and dataset (Usoskin et al.³², cancer cell lines). To systematically evaluate the embedding space, we employed Leiden clustering across a range of resolutions (0 to 1) and compared the maximum adjusted rand index (ARI) with the original cell labels (Fig. 4m,n). We observed that, compared with all other methods, scNET achieved the highest ARI in both datasets. The foundational models also demonstrated relatively weak performance on these datasets, suggesting that although they are designed to perform well on large atlas-sized datasets, their ability to distinguish cell types is reduced when applied in a zero-shot setting to unseen datasets. This highlights the need for the development of unsupervised, single-dataset frameworks as complementary approaches to large foundational models in the scRNA-seq domain.

Fig. 4: Benchmark of cell embedding and clustering.

a–f, UMAP of cell embeddings for the DRG dataset, colored by ground truth cell labels performed by scNET (a), original counts (b), scLINE (c), MAGIC (d), scGPT (e) and GeneFormer (f). g–l, UMAP of cell embeddings for the cancer cell line dataset, colored by ground truth cell labels performed by scNET (g), original counts (h), scLINE (i), MAGIC (j), scGPT (k) and GeneFormer (l). m, Maximum ARI obtained from Leiden clustering at resolutions in the range (0,1] for each method in the DRG dataset. n, Maximum ARI obtained from Leiden clustering at resolutions in the range (0,1] for each method in the cancer cell line dataset. Neuron type: NF, neurofilament; NP, nonpeptidergic; PEP, peptidergic; TH, tyrosine hydroxylase.

Upon close observation of the UMAPs, in the Usoskin dataset, we see that, in the original counts UMAP (Fig. 4b), tyrosine hydroxylase and nonpeptidergic cell types are clustered separately. However, after applying scNET, scLINE (Fig. 4a,c) and MAGIC (Fig. 4d), we observe better separation of these cell types. In the cancer cell line dataset, the original counts UMAP (Fig. 4h) shows that, whereas H228 and HCCB27 form well-defined clusters, H1975 is split into two separate communities. This separation is preserved after applying scLINE and MAGIC (Fig. 4i,j), and only scNET (Fig. 4a) successfully clusters H1975 into a single, well-defined group in its embedding.

We also investigated the distribution of attention coefficients in the KNN graph after 30 epochs (prepruning) as shown in Supplementary Fig. 8c. A notable two-peak distribution was observed, with one peak near zero (low-quality edges) and another at one (high-quality, informative edges), indicating our model’s effective differentiation between edge qualities in the KNN topology.

Finally, using a well-characterized cell cycle dataset³⁴, we examined cell state separation in UMAP representations. The original UMAP inadequately distinguished between S and G1 states, merging them into a single cluster. By contrast, UMAPs derived from our models (Supplementary Fig. 8a,b) demonstrated a clearer separation, with the S state cluster appropriately separated from the G1 and G2 clusters. This suggests a more accurate biological representation, even in the global structure. Leiden clustering in our embedding space yielded a maximum ARI of 0.46, surpassing the 0.35 ARI in the original normalized count space.

scNET reduces zero inflation and improves pathway analysis

We hypothesized that the reconstructed gene expression not only accurately reflects the original gene expression profiles but also integrates further information from the PPI network. This integration is expected to provide a more detailed characterization of pathway activation and complex biological processes in single-cell data.

To validate the quality of our reconstructed gene expression data, we first assessed whether the reconstructed gene expression accurately captures the unique expression dynamics of different cell populations. We applied scNET to the GL261a mouse brain tumor model dataset³¹, and visualized the reconstructed gene markers for different cell populations (Fig. 5a). The reconstructed cells clustered according to their cell types, demonstrating the ability of scNET ability to capture cell type distinctions. Moreover, the expression values of marker genes showed strong correlations with their respective cell populations. For instance, the expression of Cd4 and Cd8a corresponded accurately to their respective T cell subsets; Cd14 effectively identified macrophages; and P2ry12 captured microglia cells with precision.

Fig. 5: Reconstructed gene expression allows for better capture of pathway activity across different cell types and conditions in GBM tumor microenvironment.

a, Panel of reconstructed cell-type-associated marker genes. b, Heatmap of the top 20 enriched pathways for different cell types after differential gene expression analysis in scNET-reconstructed gene expression. ECM, extracellular matrix; GPI, glycosylphosphatidylinositol; NSF, N-ethylmaleimide-sensitive factor; SNARE, soluble NSF attachment protein receptor. c, Heatmap of the top 20 enriched pathways for different cell types after differential gene expression analysis in the original gene expression. NOD, nucleotide-binding oligomerization domain. d, Comparison of enriched pathways in P-selectin inhibition treatment CD8⁺ T cells compared with the control using GSEA adjustments P values. The first nine pathways are associated with T cell and immune activation (green), whereas the remaining pathways are those depleted with respect to T cell-associated genes. Akt, protein kinase B; IL, interleukin; JAK, Janus kinase; MAPK, mitogen-activated protein kinase; PD1, programmed cell death protein 1; PD-L1, programmed cell death ligand 1; PI3K, phosphatidylinositol 3-kinase; STAT, signal transducer and activator of transcription; TCA, tricarboxylic acid.

To further evaluate the reduction of zero inflation and the accuracy of marker gene expression, we calculated the AUPR for each cell type based on its respective marker gene. We compared the AUPR scores across the original counts data, scNET-reconstructed data, and the imputed data from MAGIC and DeepImpute (Table 1). Our results indicated that scNET consistently achieved higher AUPR scores across all cell types, providing strong evidence that the reconstructed data reliably captures the underlying gene expression dynamics.

Table 1 AUPR of marker gene expression for identifying different cell types

Next, we evaluated the quality of differential gene expression analysis using the reconstructed gene expression data. We hypothesized that, by incorporating the PPI network, the reconstructed gene expression would better capture differential pathways between clusters and cell populations, thereby improving biological inference. We focused on four main cell populations in the dataset: T cells, macrophages, microglia and cancer cells. We applied standard differential gene expression analysis³⁵, and the resulting differentially expressed genes for each cluster were used to calculate enriched KEGG pathways using GSEA. In Fig. 5b, we present the top 20 most enriched pathways for each cell population. Our analysis revealed that the scNET-reconstructed data captured relevant pathways associated with each population. For example, T cells were enriched in pathways such as ‘T cell receptor signaling pathway’, ‘human T cell leukemia virus 1 infection’ and ‘T_H17 cell differentiation’. Microglia showed enrichment in pathways related to their interactions with neurons, such as ‘glutamatergic synapse’ and ‘retrograde endocannabinoid signaling’. Cancer cells were enriched in proliferation and metabolism pathways such as ‘cell cycle’, ‘oxidative phosphorylation’ and ‘DNA replication’ and also in neurodegeneration-related pathways such as ‘Parkinson’s disease’, consistent with known mechanistic similarities in GBM³⁶. Macrophages were upregulated in pathways associated with their functions, such as ‘lysosome’, ‘cytokine-cytokine receptor interaction’ and ‘phagosome’, which is also shared with microglia.

For comparison, we performed the same analysis on the original gene expression data (Fig. 5c). The results indicated a strong bias toward macrophages, with significant enrichment in pathways that are not typically associated with this cell population, such as ‘apoptosis’, ‘B cell receptor signaling’ and ‘Alzheimer’s disease’. By contrast, other cell populations showed significantly fewer pathway enrichments. This suggests a bias in the original data toward macrophages, which scNET was able to correct.

Finally, we tested whether scNET’s reconstructed gene expression could identify differential dynamics within the same cell population under different biological conditions. We used a dataset that includes both control samples and samples treated with P-selectin inhibition, the treatment reduce tumor growth and improve survival in a GBM mouse model. Our analysis focused on the CD8⁺ T cell population, which, according to Yeini et al.³¹, exhibits increased tumor infiltration and activation following P-selectin inhibition. However, standard scRNA-seq analysis did not indicate notable changes at the transcriptomic level compared with the control, making this population an ideal candidate to test the ability of scNET to detect more upregulated pathways.

Given the known association between P-selectin inhibition and increased populations of activated CD8⁺ T cells, we aimed to determine whether a pathway-based approach using the scNET embedded space could reveal such associations. We selected nine KEGG pathways related to T cell activation^37,38,39,40, including pathways such as ‘T cell receptor signaling’ and ‘NF-κB’. We used the differential expression analysis on the scNET framework, alongside the original counts, to assess the differential enrichment of each pathway using GSEA²⁵. Our analysis found significant enrichment for eight of the nine T cell-related pathways within the scNET network, whereas none were detected when using the original counts.

To validate the specificity of these results, we constructed a negative set of pathways unrelated to T cells. Using the MSigDB immune signature module²⁶, we compiled a comprehensive gene repository relevant to T cells. An exhaustive search within this database identified 776 T cell-associated signatures. We selected genes present in at least 1% of these signatures and identified pathways that are depleted with respect to those genes (using a hypergeometric score). These pathways included ‘ribosome’, ‘spliceosome’ and ‘fatty acid biosynthesis’, which served as our negative set. Using the same GSEA analysis, scNET yielded lower enrichment scores relative to the original counts, indicating a high level of specificity (Fig. 5d).

Discussion

Identifying how pathways and complexes are differently activated across various biological conditions is essential for a comprehensive understanding of the biological shifts observed in comparative system analyses. In bulk RNA-seq, coexpression and differential coexpression analysis are fundamental inference tools. However, these approaches have not been as effective in scRNA-seq due to its zero-inflated nature and the diminished correlation typical of this data type. Consequently, developing innovative tools to overcome these limitations and further identify and analyze condition-specific pathway activation is vital for single-cell genomics to fully realize its considerable potential.

In this study, we introduced a cutting-edge deep learning framework, scNET, that integrates scRNA-seq data with PPI networks. Unlike traditional datasets, where the separation to samples and features is distinctly separated, our integrated dataset presents a unique duality. Here, cells are represented as vectors of gene expression measurements, and genes are characterized by vectors of expression across various cells. We posit that a model capitalizing on this dual nature will achieve superior performance.

Subsequently, we formulated a autoencoder model, which is based on a GNN architecture. Our proposed model incorporates two graphs and a node feature matrix. One network captures relationships depicted by rows, representing samples, while the other outlines relationships demonstrated by columns. Through this dual-graph encoder, values in the node feature matrix flow between the networks, enabling synchronized signal propagation among similar cells (columns) and interacting genes (rows).

To assess the effectiveness of our approach, we introduced a meticulous validation framework. This framework gauged our method’s proficiency in pinpointing pathways and functional coannotations relative to related work in the field. Our findings underscore the benefits of our approach for integrating a global biological network with context-specific gene expression. Through our model, we were able to discern distinct pathway activation within the GBM tumor microenvironment post-treatment (inhibition of P-selectin). This sheds light on the functional implications of the treatment, which remained elusive when relying solely on traditional differential gene expression analyses or coexpression analyses in the original unique molecular identifier space. This evidence propounds that our integrated embedding space offers a more insightful lens for comprehending intricate biological systems, focusing on the broader spectrum of pathways rather than individual gene expressions.

It is important to note that, although PPIs incorporate crucial information about gene interactions, they do not encompass key regulatory events that are mediated indirectly, such as those involving transcription factors. These interactions play a notable role in regulating gene expression within cells, and their inclusion is essential for a comprehensive understanding of gene–gene relationships. However, integrating them into the existing framework may not be straightforward. For instance, it is known that the expression of many transcription factors remains stable across different conditions, but their localization and phosphorylation can vary as a result of activation. These indicators obtained through technologies such as single-cell assay for transposase-accessible chromatin sequencing, could further improve the scNET embedding.

In addition, we have presented a unique approach for constructing a more refined cell–cell similarity graph. By implementing an attention mechanism on the KNN graph, we effectively pruned suboptimal edges, relaxing the underlying assumption that each cell inherently resembles a fixed set of K other cells. Although our study aimed primarily to elucidate and validate our gene embedding space, the ability of our model to accurately capture cell–cell relationships has emerged as a promising aspect. This paves the way for innovative computational methods that leverage attention mechanisms to discern cell-to-cell similarities in scRNA-seq data.

Beyond scRNA-seq, KNN is a well-established method for data imputation in machine learning⁴¹. Our proposed framework integrates this approach into its architecture, providing a more cohesive way to address noise and missing values, and enabling the model to refine the relations between different objects. Consequently, we believe our innovative framework transcends scRNA-seq data applications and can be applied to other datasets that exhibit similar dual characteristics.

Methods

Gene expression datasets

The following scRNA-seq datasets have been used in this study:

• 1. Human malaria-associated B cells: described in ref. ⁴², containing 7,044 cells over 19,374 genes.

• 2. Mouse visual cortex: described in ref. ⁴³, containing 65,540 cells over 25,187 genes.

• 3. Human cell line: described in ref. ³³, containing 902 cells over 16,468 genes from three different human cell lines (H1975, H2228, HCC827).

• 4. Mouse embryonic stem (mES) cell cycle: described in ref. ⁴⁴, containing 275 cells over 23,506 genes, each gene is labeled according to its cell cycle state (G1, G2/M, S).

• 5. GBM mouse model: described in ref. ³¹, containing 9,175 cells over 18,531 genes from control and treatment (inhibition of P-selectin) samples.

• 6. Usoskin’s DRG: described in ref. ³², containing 799 cells over 25,334 genes from the DRG of the mouse identified by known markers associated with their function.

• 7. Glioma tumor-reactive CD8⁺ T cells: as described in ref. ⁴⁵, this dataset contains 4,231 T cells over 14,202 genes from the mouse glioma tumor microenvironment. All T cells were H-2Kb-SIINFEKL dextramer-positive (Dext⁺).

Data prepossessing

scRNA-seq expression data was preprocessed using standard Scanpy package³⁵ pipeline (v.1.9.1). In brief, the pipeline consists of the following steps:

• 1. log normalization: feature counts for each cell are divided by the total counts for that cell and multiplied by a scale factor, finally log₁p is applied.

• 2. Variance-based filtering: scNET learns to reconstruct a subset of expressed genes that exhibit high variance across the dataset, as described below. To identify these genes, we used the highly_variable_genes function, which calculates gene-wise variance after mean normalization. The default cutoff was applied to obtain the final subset of highly variable genes.

• 3. Dimensionality reduction: principal component analysis and UMAP are calculated from the scale-normalized data matrix, where each feature normalized expression is scaled across the cells. The number of principal components for the clustering was selected manually based on an elbow plot showing the gain in variance with each further vector.

• 4. KNN graph: KNN was calculated for each cell in the data and a KNN graph was constructed in the reduced principal component analysis space.

• 5. Scaling: we found that our model works best with scaled gene expression data. Therefore, we applied standard scaling to the log-normalized expression, where each gene’s expression is normalized to have a mean of 0 and s.d. of 1.

A weighted human PPI was used⁴⁶, filtering edges with scores lower than 0.5. The filtered network spans 14,136 proteins and 111,790 interactions. We further removed all nodes corresponding to genes that were not expressed in the scRNA data (zero expression across all the cells). To construct the node feature matrix from the normalized gene expression matrix, we filtered out genes that were not represented by an edge in the network or were not expressed in the scRNA data.

The encoder

Our proposed model integrates scRNA-seq and PPI data by learning a gene and cell embeddings that effectively capture both the network structure and the expression information while also reducing the noise level of the data. Specifically, our encoder architecture (Fig. 1) consists of alternately applying a convolution layer to aggregate information between similar cells, therefore impute missing values and reducing noise level, and then applying another convolution layer on the transposed matrix to aggregate information between interacting proteins. The aggregated information is then passed through a graph attention layer to produce the latent representation.

Graph convolution layer

A convolution layer⁴⁷ aggregates for every node information from neighboring nodes to form the output node feature vector. Formally, we can define G = (V, E) with N = ∣V∣ nodes and adjacency matrix A ∈ R^N×N and node feature matrix X ∈ R^N×F. The output of a single convolution layer is $\sigma (\hat{A}\delta (X\,)W\,)$, where σ is the activation function, δ is the dropout and $\hat{A}={\bar{D}}^{-1/2}\bar{A}{\bar{D}}^{-1/2}$, D is the diagonal degree matrix of the graph and $\bar{A}=A+I$.

Graph attention layer

By incorporating an attention mechanism, our model refines the cell–cell similarity graph (KNN) by learning a weight for each edge in the graph. These weights represent the importance the model assigns to cell j when reconstructing the gene expression of cell i. We argue that the assumption that each cell is similar to a fixed number K of other cells is arbitrary and can lead to the inclusion of false edges. Therefore, in our framework, we use the learned attention weights as a basis for pruning low-quality edges.

Formally, for an input feature matrix $X\in {{\mathbb{R}}}^{N\times F}$, an attention layer⁴⁸ aggregates information from all nodes to score a given node, accounting for network proximities. For a node i with degree d, we define:

$$\bf{{x}_{i}^{{\prime}} }={W}_{1}\bf{{x}_{i}}+\sum _{j\in N(i)}{\alpha }_{i,\,j}{W}_{2}\bf{{x}_{j}},$$

where N(i) are the neighbors of node i in the network and the attention coefficient is:

$${\alpha }_{i,\,j}=\,\text{sigmoid}\,\left(\frac{{({W}_{3}\bf{{x}_{i}})}^{T}\cdot ({W}_{4}\bf{{x}_{j}})}{\sqrt{d}}\right),$$

and W₁, W₂, W₃ and W₄ are learned matrices.

In our implementation, we have modified the original activation function, replacing the node-wise softmax with a sigmoid function. This change means that the scores for the edges are not normalized by node, allowing us to prune global low-scoring edges as described below.

KNN graph pruning using attention coefficients

Using KNN to smooth expression across cells assumes that each cell is similar to an arbitrary K other cells in the dataset. However, this assumption may not be biologically accurate, as cells from different populations and states may be represented in varying numbers within the data. To address this, we propose using the learned attention coefficients to prune low-quality edges. Specifically, we compute and define the new edge set of the graph as:

$${E}^{{\prime} }=\{(i,j)| (i,j)\in E\,\,\text{and}\,\,{\alpha }_{i,\,j} > \beta \}$$

where P₁₀ is the 10th percentile and β is defined as $\max (0,{P}_{10})$.

As a result, the introduction of the attention layer not only helps the model to learn more meaningful latent representations for cells and genes but also allows the model to learn a new topology for the KNN network, enabling the graph to better capture cell–cell relations.

The complete autoencoder model

Our final autoencoder model is depicted in Fig. 1. First, the KNN graph, PPI network and gene expression matrix are fed into a three-layer dual-view encoder (three layers of the graph convolutional network of the cell and three layers of the graph convolutional network of the gene). Next, we utilize a single layer of graph attention to learn two dense latent representations (using the KNN graph for the cell attention layer and the PPI for the gene attention layer), one for the genes and another for the cells. Finally, we apply an inner product decoder to reconstruct the PPI network and a three-layer fully connected decoder to reconstruct the gene expression.

At fixed intervals during training, we also prune the KNN graph as discussed above. After training, the model returns the embeddings of the genes and cells, along with the pruned KNN graph and the reconstruction of the gene expression. The loss function combines PPI reconstruction and gene expression reconstruction losses.

The inner product decoder is defined to be $\hat{A}=\sigma (Z{Z}^{T})$ where Z is the latent representation of the genes and σ is the Sigmoid activation function. We denote with Z_pos the set of edges in the trained PPI network, and with Z_neg the set of randomly sampled negative edges s.t ∣Z_pos∣ = ∣Z_neg∣. We then define:

$${{\mathcal{L}}}_{\rm{PPI}}=-\mathop{\sum}\limits_{z\in {Z}_{\rm{pos}}}{\rm{log}}(z)-\sum _{{z}^{{\prime} }\in {Z}_{\rm{neg}}}\rm{log}(1-{\it{z}}^{{\prime} })$$

As described above, we first select a subset of genes that exhibit substantial variation across the dataset. We denote this subset as M_v. We then use the mean square error (m.s.e.) loss function on the genes in this subset to train the model. Formally, we define:

$${{\mathcal{L}}}_{v}=\,\text{m.s.e.}\,\left(\bf{{M}_{{\mathrm{v}}}},\hat{{{\bf{M}}}_{{\mathrm{v}}}}\right)$$

where $\hat{{{\bf{M}}}_{{\mathrm{v}}}}$ is the reconstructed vector of expression levels of the genes in M_v.

Our final loss function is:

$${\mathcal{L}}={\lambda }_{\rm{PPI}}{{\mathcal{L}}}_{\rm{PPI}}+{\lambda }_{{\mathrm{v}}}{{\mathcal{L}}}_{{\mathrm{v}}}$$

Where λ_PPI and λ_v are hyper-parameters of the model.

Network evaluation

To assess the predictive power of various networks in our research, we focused on known functionality groups, such as those defined in KEGG pathways. Generally, each group was divided into training and test sets with a ratio of two-thirds to one-third. We then applied random walk with restart approach⁴⁹ to propagate membership from the training group to all other nodes. The propagation scores were used as membership scores to calculate area under the curve (AUC) scores for each network. In detail, given the adjacency matrix W and the node degree matrix D, the propagation is iteratively computed using the following formula:

$$\bf{{F}^{\,t+1}}=\alpha {W}^{{\prime} }\bf{{F}^{\,t}}+(1-\alpha )\bf{{F}^{\,0}}$$

where F⁰ represents the input binary membership vector and ${W}^{{\prime} }={D}^{-1/2}W{D}^{-1/2}$ is the normalized adjacency matrix of the network. To account for node centrality, we normalize the resulting vector F^∞ by dividing it entry-wise with the propagation scores obtained with an all − 1 input vector.

Furthermore, for the evaluation of networks with different numbers of edges, we implemented a topology-free evaluation framework, comparing the predictive power of each network against a set of random permutation graphs, as outlined previously³⁰. A database of 230 gene lists associated with various diseases was employed for this purpose. For each network, we generated 30 degree-preserving random networks to establish a background distribution. The gene lists were split into training and test sets, and network propagation seeded by the training set was employed to predict the test set. An AUC score was calculated for each network and transformed into a z score using the distribution of scores on the randomized networks.

Implementation and training

The model was implemented using the Python and PyTorch⁵⁰ (v.2.1.1) deep learning framework. Specifically, the graph convolution layers were implemented using the torch-geometric package⁵¹ (v.2.1.1). To optimize the model during the training process, the Adam optimizer with a learning rate of 0.0001 was used with L₂ regulation of 1 × 10⁻⁵.

The model was trained in Google Colab Pro+ platform using NVIDIA A100 40 GB random-access memory graphics processing unit. Training process comprised 250 epochs and, after every 10 epochs, AUROC values were calculated. At each stage, we saved the model and the KNN network that achieved the highest AUC score on the test set. The KNN network was pruned every 30 epochs at a maximum rate of 10% during each pruning. To avoid disconnection of cells from the graph each cell maintained at least five edges in the pruned graph.

To determine the hyperparameter values, we utilized a reference dataset⁴² and performed cross-validation using the receiver operating characteristic curve as the evaluation metric. We found that balancing the loss between PPI reconstruction and gene expression was optimal. Pruning exceeding 10% also resulted in a decline in performance. Finally, we observed that three layers of the expression decoder yielded the best result. The robustness of the model was further demonstrated by training it on more datasets, yielding consistent results.

The dimensions of the encoder are determined by the number of genes and cells in the dataset. Since the number of genes remains relatively consistent across different datasets, the primary variable becomes the number of cells. In an effort to reduce space complexity and introduce greater randomization during training, we propose a strategy of randomly splitting the edges of the KNN graph into mini-batches. Each batch utilizes a fraction of the original edges, typically one of five or one of ten, depending on the dataset size. This approach effectively lowers the random-access memory usage during training, while maintaining adequate performance.

For datasets with a relatively larger number of cells (above 10,000), the size of the model becomes too large for standard graphics processing units. Consequently, in such scenarios, we divide the cells into independent subsets (or mini-batches) to be processed iteratively. In this setting, a new integrated pruned KNN graph will not be generated, but the model still learns to embed the cells into a unified space, incorporating refined cell–cell relations. We show that there is no notable batch effect following this process (Supplementary Fig. 1). For datasets containing fewer than 100,000 cells, we typically divide the data into ten subsets.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.